VERY QUICK SETUP of LeNet-5 for Handwritten Digit Classification Using Nvidia-Docker 2.0 + CUDA + CuDNN + Jupyter Notebook + Caffe
In this story, we will have a VERY QUICK SETUP of a LeNet-5 for digit classification using Nvidia-Docker 2.0 + Caffe with GPU acceleration. (Sik-Ho Tsang @ Medium)
In this story, we will cover:
- Caffe File Structure
- Running the Docker
- Training and Testing of the LeNet-5
Thus, It is assumed to we’ve already installed Ubuntu + GPU driver + Docker + Nvidia-Docker 2.0, and known how to run the Caffe Docker image. If you are interested about this part, please follow this story:
VERY QUICK SETUP of CaffeNet (AlexNet) for Image Classification Using Nvidia-Docker 2.0+ CUDA + CuDNN + Jupyter Notebook + Caffe
In brief, one advantage of using Docker is that, we don’t need to process the tedious installation for CUDA, CuDNN, Caffe, in which the installation failure may occur due to the wrong step, hardware, or version compatibility problem.
Another advantage is to have numerous Docker working together within the same physical computer with different versions of software installed.
1. Caffe File Structure

Basically, in Caffe, we just need to handle the prototxt just like a set of configuration files. By changing the settings of the configuration files, we can already modify or create our own deep neural network structure.
solver.prototxt
Includes the paths of train.prototxt and test.prototxt, as well as the backpropagation parameters such as the learning rate policy and momemtum.
train.prototxt
Includes network structure such as the layer type (convolution, pooling, fully connected), kernal size, stride, and the weight intialization.
test.prototxt
Similar to train.prototxt but the dataset is the testing dataset such as weight initialization because it is used for testing only, not for training.
2. Running the Docker
Run the latest Caffe Docker image:
sudo docker run --runtime=nvidia -it -p 8888:8888 bvlc/caffe:gpu bashRun the Jupyter Notebook:
pip install --upgrade pip
pip install jupyter
jupyter notebook --allow-root --ip=0.0.0.0At the host, there is a HTTP path at the end, we can access the Jupyter Notebook at the host by:
http://<container>:8888/?token=<token>or
http://127.0.0.1:8888/?token=<token>3. Training and Testing of the LeNet-5
At the host, we can launch the Firefox, and enter the above HTTP path with token to access the Jupyter Notebook. We should at root directory:
There is a tutorial provided by Caffe. We can go to \opt\caffe\examples.
Then open the notebook file 01-learning-lenet.ipynb:

There are already many comments to describe the notebook. The rough steps are:
- Download the dataset and convert it as lmdb format.
- Prepare the solver.prototxt, train.prototxt, test.prototxt.
- Check the LeNet-5 network structure.
- Training and Testing the LeNet by backpropagation.
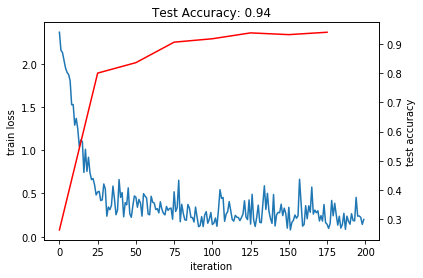
Since there are only 2 Conv + 2 Pool + 1 FC, the training is ultimately fast. (But I believe it was very slow at that moment since this is a paper published in 1989.) And that’s also the reason why it is called LeNet-5. After the training, we should can see that the test accuracy have already got 94%.
There are also some interesting findings:
For the digit 7, before softmax, along the training iteration, there are many grey areas meaning that the probabilities are among the digits from 0 to 10 are still having some non-zero values especially for digit 9.


After softmax, we can see that most of them are black (close to zero) except the one at digit 7 is white. This means that softmax has magnified the correct results and suppress the other results, which can somehow help for accelerating the convergence during backpropagation.

Another interesting fact is that, for some strange written digit, such as digit 9, the probability of classifying as 4 is very close to that of 9. This is because there are only 2 Conv layers which are not enough to have some more difficult classification situations.


Nevertheless, it is really amazing there have had already LeNet-5 invented in the year of 1989, which is a year with very immature development of CPU and GPU, no CUDA, and no deep learning framework such as Caffe, etc, where backpropagation should be done my own self.
References
Paper:
[1989 NIPS] [LeNet-5]
Handwritten Digit Recognition with a Back-Propagation Network
[1998 Proc IEEE] [LeNet-5]
Gradient-based learning applied to document recognition
[2014 ACMMM] [Caffe]
Caffe: Convolutional Architecture for Fast Feature Embedding
To know more about Docker:
Docker Tutorial 1: Docker Installation in Ubuntu 18.04
Docker Tutorial 2: Pulling Image
Docker Tutorial 3: Running Image
Docker Tutorial 4: Exporting Container and Saving Image
Docker Tutorial 5: Nvidia-Docker 2.0 Installation in Ubuntu 18.04
