Review — Sparse MLP for Image Recognition: Is Self-Attention Really Necessary?
sMLPNet, On Par With or Even Better Than Swin Transformer
Sparse MLP for Image Recognition: Is Self-Attention Really Necessary?,
sMLPNet, by Microsoft Research Asia, and University of Science and Technology of China,
2022 AAAI, Over 20 Citations (Sik-Ho Tsang @ Medium)
Image Classification, MLP, Vision Transformer, ViT
- An attention-free network called sMLPNet is proposed, which is based on the existing MLP-based vision models.
- Specifically, the MLP module in the token-mixing step is replaced with a novel sparse MLP (sMLP) module. For 2D image tokens, sMLP applies 1D MLP along the axial directions and the parameters are shared among rows or columns.
- By sparse connection and weight sharing, sMLP module significantly reduces the number of model parameters and computational complexity, avoiding over-fitting.
Outline
- sMLPNet Overall Architecture
- Sparse MLP Module
- Ablation Studies
- SOTA Comparisons
1. sMLPNet Overall Architecture

1.1. Input
- Similar to ViT, MLP-Mixer, and recent Swin Transformer, an input RGB image with spatial resolution H×W is divided into non-overlapping patches by a patch partition module.
- A small patch size of 4×4 is adopted at the first stage of the network. Each patch is first reshaped into a 48-dimensional vector, and then mapped by a linear layer to a C-dimensional embedding.
1.2. Backbone
- The entire network is comprised of four stages. Except for the first stage, which starts with a linear embedding layer, other stages start with a patch merging layer which reduces the spatial dimension by 2×2 and increases the channel dimension by 2 times.
- The patch merging layer is simply implemented by a linear layer which takes the concatenated features of each 2×2 neighboring patches as input and outputs the features of the merged patch.
- Then, the new image tokens are passed through a token-mixing module (Figure (b)) and a channel-mixing module. These two modules do not change the data dimensions.
1.3. Token-Mixing Module
- The token-mixing module take advantage of locality bias by using a depth-wise convolution (DWConv) with kernel size 3×3.
- Batch normalization (BN) and skip connections are applied in a standard way.
The proposed Sparse MLP (sMLP) is proposed to replace the original one here (described in the next section).
1.4. Channel-Mixing Module
2. Sparse MLP Module
2.1. Conceptual Idea

- (a) MLP: The token in dark orange interacts with all the other tokens in a single MLP layer.
(b) sMLP: In contrast, in one sMLP layer, the dark-orange token only interacts with horizontal and vertical tokens marked in light orange.
The interaction with all the other white tokens can be achieved when sMLP is executed twice.
- (The cross-shaped interaction is similar to the cross-shaped attention in CSwin Transformer.)
2.2. Implementation

It consists of three branches: two of them are responsible for mixing information along horizontal and vertical directions respectively and the other path is the identity mapping.
The output of the three branches are concatenated and processed by a pointwise convolution to obtain the final output.
- Specifically, let Xin of size H×W×C denote the collection of input tokens.
- In the horizontal mixing path, the data tensor is reshaped into HC×W, and a linear layer with weights W_W of size W×W is applied to each of the HC rows to mix information.
- Similar operation is applied in the vertical mixing path and the linear layer is characterized by weights W_H of size H×H.
- Finally, the output from the three paths are fused together:

- (The cross-shaped interaction implementation is similar to the cross-shaped attention implementation in CSwin Transformer.)
2.3. Complexity Analysis
- The complexity of one sMLP module is:

- While the complexity of token mixing part in MLP-Mixer is:

We can see that MLP-Mixer cannot afford a high-resolution input or the pyramid processing, as the computational complexity grows with N².
In contrast, the computational complexity of the proposed sMLP grows with N√N.
2.4. Model Variants
- Three variants of our model, called sMLPNet-T, sMLPNet-S sMLPNet-B to match with the model size of Swin-T, Swin-S, and Swin-B, respectively. The expansion parameter in the FFN for channel mixing is α=3 by default. The architecture hyper-parameters of these models are:

3. Ablation Studies

- The DWConv operation is extremely lightweight. When removing it from sMLPNet (Global only), the model size only changes from 19.2M to 19.1M and the FLOPs only decrease by 0.1B. However, the image recognition accuracy significantly drops to 80.6%.
By removing sMLP, it becomes the local only version and only achieves an accuracy of 80.7.

- Authors start to remove sMLP from stage 1 until stage 4.
The top-1 accuracy decreases as removing sMLP module from more stages.
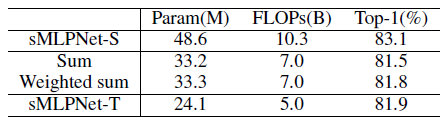
- Compared to baseline, which has 48.6M parameters and 10.3B FLOPs, the two alternative fusion methods bring much fewer parameters and FLOPs.
But the image recognition accuracy also drops from 83.1% to 81.5% and 81.8%.
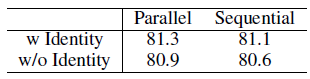
- Sequential processing is tried on the Sparse MLP Module.
Using identity mapping always brings better results. Parallel processing is always better than sequential processing.

- A tiny sMLPNet model (* means α=2) is taken. And all the sMLP blocks in stage 2, 3, and 4 are replaced with the normal MLP blocks. The sMLP blocks in stage 1 is replaced by DWConv, as MLP blocks are too heavy to be used in stage 1. This is referred to as the multi-stage MLP model.
We can see that the top-1 accuracy of multi-stage MLP is only 77.8%, with 3.5% performance loss with respect to the base sMLPNet-T model.
4. SOTA Comparisons

- Among these existing models, Swin Transformer performs the best.
The proposed model, despite the fact that it belongs to the MLP-like category, performs on par with or even better than Swin Transformer.
- In particular, sMLPNet-T achieves 81.9% top-1 accuracy, which is the highest among the existing models with FLOPs fewer than 5B.
- The performance of sMLPNet-B is also very impressive. It achieves the same top-1 accuracy as Swin-B, but the model size is 25% smaller (65.9M vs. 88M) and the FLOPs are nearly 10% fewer (14.0B vs. 15.4B).
- Remarkably, there is no sign of over-fitting, which is the main problem that plagues the MLP-like methods, when the model size grows to nearly 66M.
This shows that an attention-free model could attain SOTA performance, and the attention mechanism might not be the secret weapon in the top-performing Transformer-based models.
Reference
[2022 AAAI] [sMLPNet]
Sparse MLP for Image Recognition: Is Self-Attention Really Necessary?
1.1. Image Classification
1989 … 2022 [ConvNeXt] [PVTv2] [ViT-G] [AS-MLP] [ResTv2] [CSWin Transformer] [Pale Transformer] [Sparse MLP]