Review — SASA: Stand-Alone Self-Attention in Vision Models
Self-Attention Blocks Replace Convolutional Blocks in ResNet

Stand-Alone Self-Attention in Vision Models
SASA, by Google Research, Brain Team
2019 NeurIPS, Over 400 Citations (Sik-Ho Tsang @ Medium)
Self-Attention, Image Classification, Object Detection
- In convention, attention blocks are built on top of convolutions.
- Self-attention block is designed to replace convolutional block.
- Fully attentional vision model is developed.
Outline
- Convolution Block
- Self-Attention Block
- SASA: Fully Attentional Vision Models
- Experimental Results
1. Convolution Block

- Given a learned weight matrix W ∈ R^(k×k×dout×din), the output yij ∈ R^(dout) for position ij is defined by spatially summing the product of depthwise matrix multiplications of the input values:

- where Nk(i, j) is the neighborhood region based on the kernel size k.
2. Self-Attention Block
2.1. Single-Headed Attention

- Similar to a convolution, given a pixel xij ∈ R^(din), a local region of pixels is firstly extracted in positions ab ∈ Nk(i, j) with spatial extent k centered around xij, which called the memory block.
- This form of local attention differs from prior work exploring attention in vision which have performed global (i.e., all-to-all) attention between all pixels.
- Single-headed attention for computing the pixel output yij ∈ R^(dout) is then computed as follows (see the above figure):

- where the queries qij = WQ xij , keys kab = WK xab, and values vab = WV xab are linear transformations of the pixel in position ij and the neighborhood pixels. softmaxab denotes a softmax applied to all logits computed in the neighborhood of ij. WQ, WK, WV ∈ R^(dout×din) are all learned transforms.
- This computation is repeated for every pixel ij.
2.2. Multiple Attention Heads
- In practice, multiple attention heads are used to learn multiple distinct representations of the input.
- It works by partitioning the pixel features xij depthwise into N groups xnij ∈ R^(din/N), computing single-headed attention on each group separately as above with different transforms WnQ, WnK, WnV ∈ R^(din×dout/N) per head, and then concatenating the output representations into the final output yij ∈ R^(dout).
2.3. Positional Information

- As currently framed, no positional information is encoded in attention, which makes it permutation equivariant, limiting expressivity for vision tasks.
- Sinusoidal embeddings based on the absolute position of pixels in an image (ij) can be used [25], but early experimentation suggested that using relative positional embeddings [51, 46] results in significantly better accuracies.
- Instead, attention with 2D relative position embeddings, relative attention, is used.
- Relative attention starts by defining the relative distance of ij to each position ab ∈ Nk(i, j). The relative distance is factorized across dimensions, so each element ab ∈ Nk(i, j) receives two distances: a row offset a−i and column offset b−j (see the above figure).
- The row and column offsets are associated with an embedding ra−i and rb−j respectively each with dimension 0.5*(dout). The row and column offset embeddings are concatenated to form r_(a−i,b−j). This spatial-relative attention is now defined as:
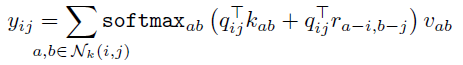
Thus, the logit measuring the similarity between the query and an element in Nk(i, j) is modulated both by the content of the element and the relative distance of the element from the query.
2.4. Parameter & Computational Efficiency
- The parameter count of attention is independent of the size of spatial extent, whereas the parameter count for convolution grows quadratically with spatial extent.
- The computational cost of attention also grows slower with spatial extent compared to convolution with typical values of din and dout.
- For example, if din = dout = 128, a convolution layer with k = 3 has the same computational cost as an attention layer with k = 19.
3. SASA: Fully Attentional Vision Models
- There are two main parts in ResNet: Residual blocks & stem.
3.1. Replacing Spatial Convolutions
- The core building block of a ResNet is a bottleneck block with a structure of a 1×1 down-projection convolution, a 3×3 spatial convolution, and a 1×1 up-projection convolution, followed by a residual connection between the input of the block and the output of the last convolution in the block.
- The proposed transform swaps the 3×3 spatial convolution with a self-attention layer. All other structure, including the number of layers and when spatial downsampling is applied, is preserved. This transformation strategy is simple but possibly suboptimal.
3.2. Replacing the Convolutional Stem
- In a ResNet, the stem is a 7×7 convolution with stride 2 followed by 3×3 max pooling with stride 2. This property makes learning useful features such as edge.
- Using self-attention form in the stem underperforms compared to using the convolution stem of ResNet.
- A distance based information is injected in the pointwise 1×1 convolution (WV) through spatially-varying linear transformations:
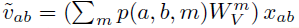
- WmV are combined through a function of the position of the pixel in its neighborhood p(a, b, m). (See appendix of paper for more details.) The position dependent factors are similar to convolutions, which learn scalar weights dependent on the pixel location in a neighborhood. The stem is then comprised of the attention layer with spatially aware value features followed by max pooling.
3.3. Model
- ResNet-50 is used as baseline.
- The multi-head self-attention layer uses a spatial extent of k = 7 and 8 attention heads.
- The position-aware attention stem as described above is used. The stem performs self-attention within each 4×4 spatial block of the original image, followed by batch normalization and a 4×4 max pool operation.
- To scale the model, for width scaling, the base width is linearly multiplied by a given factor across all layers.
- For depth scaling, a given number of layers are removed from each layer group.
- The 38 and 26 layer models remove 1 and 2 layers respectively from each layer group compared to the 50 layer model.
4. Experimental Results
4.1. ImageNet

Compared to the ResNet-50 baseline, the full attention variant achieves 0.5% higher classification accuracy while having 12% fewer floating point operations (FLOPS) and 29% fewer parameters.
- Furthermore, this performance gain is consistent across most model variations generated by both depth and width scaling.
4.2. COCO Object Detection

- RetinaNet is used as baseline. Self-attention is used by making the backbone and/or the FPN and detection heads fully attentional.
- Using an attention-based backbone in the RetinaNet matches the mAP of using the convolutional backbone but contains 22% fewer parameters.
- Furthermore, employing attention across all parts of the model including the backbone, FPN, and detection heads matches the mAP of the baseline RetinaNet while using 34% fewer parameters and 39% fewer FLOPS.
4.3. Further Studies

The best performing models use convolutions for early groups and attention for later groups.
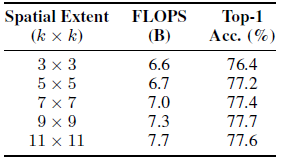
Small k perform poorly, but the improvements of larger k plateaus off.

Relative encodings significantly outperform other strategies.

Using just q⊤r interactions only drops accuracy by 0.5%.

The proposed attention stem outperforms stand-alone attention by 1.4% despite having a similar number of FLOPS.
Spatially-aware value attention outperforms both stand-alone attention and values generated by a spatial convolution.
Reference
[2019 NeurIPS] [SASA]
Stand-Alone Self-Attention in Vision Models
Image Classification
1989–2018 … 2019: [ResNet-38] [AmoebaNet] [ESPNetv2] [MnasNet] [Single-Path NAS] [DARTS] [ProxylessNAS] [MobileNetV3] [FBNet] [ShakeDrop] [CutMix] [MixConv] [EfficientNet] [ABN] [SKNet] [CB Loss] [AutoAugment, AA] [BagNet] [Stylized-ImageNet] [FixRes] [SASA]
2020: [Random Erasing (RE)] [SAOL] [AdderNet]
2021: [Learned Resizer]
