Brief Review — ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks

ECA-Net, Outperforms SENet With Lower Complexity

4 min readApr 9, 2023

--

**Comparison of various attention modules (i.e.,** **SENet**, **CBAM, A2-Nets [4] and ECA-Net) using** **ResNets as backbone models**

ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks,
ECA-Net, by Tianjin University, Dalian University of Technology, and Harbin Institute of Technology
2020 CVPR, Over 1900 Citations (Sik-Ho Tsang @ Medium)
Image Classification
1989 … 2022 [ConvNeXt] [PVTv2] [ViT-G] [AS-MLP] [ResTv2] [CSWin Transformer] [Pale Transformer] [Sparse MLP] [MViTv2] [S²-MLP] [CycleMLP] [MobileOne] [GC ViT] [VAN] [ACMix] [CVNets] [MobileViT] [RepMLP] [RepLKNet] [ParNet] 2023 [Vision Permutator (ViP)]
==== My Other Paper Readings Are Also Over Here ====

ECA-Net is proposed, where a local cross-channel interaction strategy without dimensionality reduction is used, which can be efficiently implemented via 1D convolution.
A method is developed to adaptively select kernel size of 1D convolution, determining coverage of local cross-channel interaction.

Outline

SENet Variants
ECA-Net
Results

1. SENet Variants

**Comparison of various channel attention modules using** **ResNet-50 as backbone model on ImageNet.**

1.1. SENet

Channel attention of SE block in SENet is:

where σ is sigmoid. W is learnable weights/layers, and y=g(X) which is global average pooling (GAP):

In SENet, 2 FC layers with dimension reduction and expansion are used:

1.2. SENet Variants

SE-Var1 with no parameter is tried, and is still superior to the original network.
SE-Var2 learns the weight of each channel independently, which is slightly superior to SE block while involving less parameters.

SE-Var3 employing one single FC layer performs better than two FC layers with dimensionality reduction in SE block.

Wvar2 for SE-Var2 is a diagonal matrix, involving C parameters; Wvar3 for SE-Var3 is a full matrix, involving C² parameters.

1.3. Group Convolution (GC)

One extension of Wvar2 is a block diagonal matrix:

which is implemented using SE block with group convolutions (SE-GC) and it is indicated by σ(GCG(y))=σ(WGy).

Yet, excessive group convolutions will increase memory access cost and so decrease computational efficiency. SE-GC with varying groups have bring no gains, as shown in the above table. This might be due to the fact that SE-GC completely discards dependences among different groups.

2. ECA-Net

2.1. ECA Module

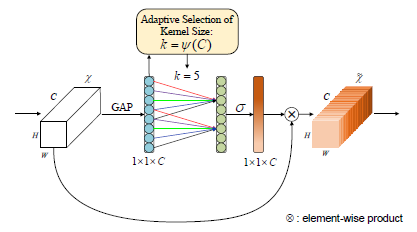
**Diagram of our efficient channel attention (ECA) module.**

Based on the above analysis, ECA module is designed where each parameter.
The weight of yi is calculated by only considering interaction between yi and its k neighbors, i.e.:

By sharing the parameters, indeed, it is a 1D convolution (C1D):

ECA module with k=3 achieves similar results with SE-var3 while having much lower model complexity.

2.2. Adaptive Kernel Size

The coverage of interaction (i.e., kernel size k of 1D convolution) is proportional to channel dimension C. In other words, there may exist a mapping Φ between k and C:

The simplest way is a linear function γ*k-b.
A non-linear way is:

Thus, given channel dimension C, kernel size k can be adaptively determined by:

where γ=2 and b=1.

3. Results

3.1. ECA-Net Performance

**Results of our ECA module with various numbers of k using** **ResNet-50 and** **ResNet-101 as backbone models.**

ECA-Net clearly outperforms SENet, and also outperforms fixed kernel version of ECA-Net.

3.2. Different Backbones on ImageNet

**Comparison of different attention methods on ImageNet**

ECA-Net is superior to SENet and CBAM while it is very competitive to AA-Net with lower model complexity. Note that AA-Net is trained with Inception data augmentation and different setting of learning rates.